工具介绍

一元二次方程计算器是一款专为解决一元二次方程设计的数学工具。它能够快速准确地计算出方程的根，无论是实数根还是复数根。用户只需输入方程的系数（a, b, c），计算器即可自动完成求解过程，并显示详细的解题步骤。这款工具不仅适用于学生和教师，也适合需要频繁处理一元二次方程的专业人士。其简洁直观的操作界面和强大的计算功能，使得复杂的数学问题变得简单易解。一元二次方程计算器是学习、教学和科研工作中的得力助手。

工具界面展示

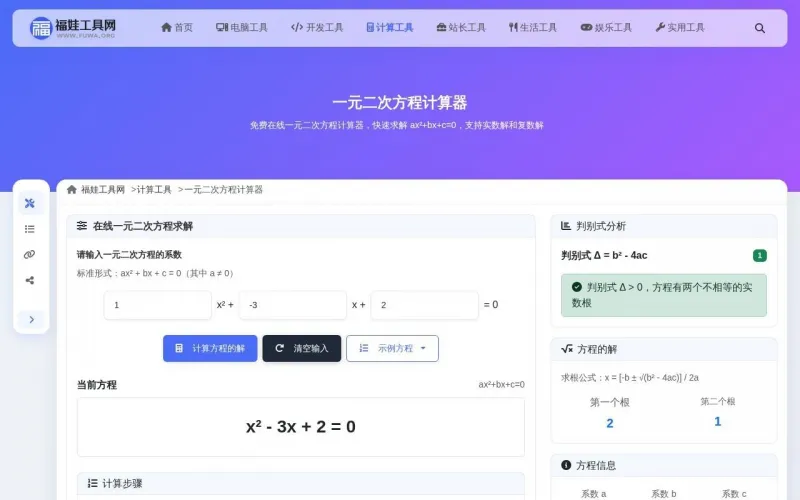
功能特色

实时计算：输入系数后自动计算方程的解
详细步骤：显示完整的计算过程，帮助理解求解原理
判别式分析：直观展示判别式大小，判断根的类型
示例方程：提供多种类型的示例方程，方便学习参考
复数根支持：支持计算和显示复数根
美观界面：采用现代化设计，使用方便，视觉舒适

使用方法

输入系数：在对应输入框中输入一元二次方程的系数a、b、c
查看方程：实时显示当前输入的方程形式，确保输入正确
点击计算：点击"计算方程的解"按钮获取结果
查看结果：在右侧面板查看计算结果、判别式分析和详细步骤
使用示例：点击"示例方程"下拉菜单，选择预设的示例方程进行学习

适合人群

学生：学习一元二次方程求解的学生
教师：需要演示方程求解过程的教师
工程师：需要快速求解方程的工程师
数学爱好者：对数学计算感兴趣的爱好者
普通用户：任何需要求解一元二次方程的用户

常见问题解答(FAQ)

系数a可以为0吗？

不能。如果a=0，方程就退化为一元一次方程，不再是二次方程。

一元二次方程的标准形式是什么？

一元二次方程的标准形式是：ax² + bx + c = 0（其中 a ≠ 0），a、b、c 是常数，x 是未知数。

什么是判别式？

判别式是一元二次方程中的一个重要概念，计算公式为 Δ = b² - 4ac。通过判别式的值可以判断方程根的情况：Δ > 0 时有两个不相等的实数根，Δ = 0 时有两个相等的实数根，Δ < 0 时有两个共轭复数根。

支持复数解吗？

是的，当判别式 Δ < 0 时，工具会自动计算并显示复数根，形式为 a + bi，其中 i 是虚数单位。

如何使用示例方程？

您可以点击"示例方程"下拉菜单，选择一个示例方程，系统会自动填充系数并计算结果。

如何使用求根公式？

求根公式是一元二次方程的通用解法，公式为：x = [-b ± √(b² - 4ac)] / (2a)。其中，± 表示有两个解，√ 表示平方根运算。