工具介绍
正态分布计算器是一款免费、专业的在线统计工具,用于计算正态分布的概率密度函数、累积分布函数和分位数。支持数据导入自动计算均值和标准差,提供直观的可视化图表,并支持多种格式导出。无需安装,数据本地处理,适用于统计学研究、数据分析、教育教学等多种场景。兼容 Chrome、Edge、Firefox 等主流浏览器。
工具界面展示
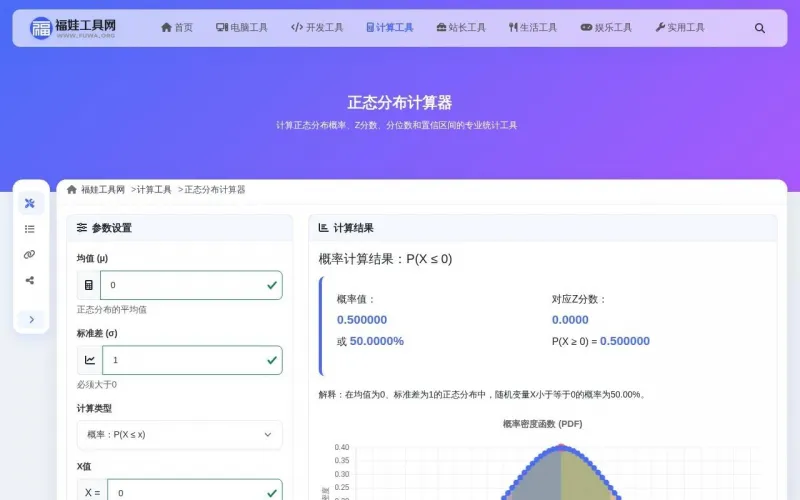
功能亮点
- 多种计算类型:支持概率密度、累积概率、分位数、区间概率和双尾检验
- 数据导入功能:支持上传CSV/TXT文件自动计算均值和标准差
- 可视化图表:提供概率密度函数和累积分布函数的直观图表
- 实时计算:支持实时自动计算,无需手动刷新结果
- 导出功能:支持导出结果和图表,方便进一步分析
- 经验法则显示:内置68-95-99.7经验法则卡片
- 本地处理:所有数据在浏览器本地处理,保护数据安全
- 免费使用:完全免费,无需注册,随时可用
使用方法
- 输入参数:在左侧输入框中输入正态分布的均值和标准差
- 选择计算类型:选择计算类型:概率密度(PDF)、累积概率(CDF)或分位数
- 输入数值:输入相应的数值(如X值或概率值)
- 执行计算:点击"计算"按钮查看结果
- 数据导入:可选择导入数据文件自动计算均值和标准差
- 查看图表:查看可视化图表,可下载结果或图表
适合人群
- 统计学研究人员和学生:用于统计学研究和学习
- 数据分析和数据科学家:在数据分析中应用正态分布
- 教育工作者和教师:用于教学和演示正态分布概念
- 金融分析师和风险管理人员:评估金融风险和概率
- 质量控制和可靠性工程师:进行质量控制和可靠性分析
- 专业人士:任何需要进行正态分布计算的专业人士
常见问题解答(FAQ)
什么是正态分布?
正态分布,也称为高斯分布,是一种连续概率分布,其概率密度函数呈钟形曲线。许多自然现象和测量结果都近似服从正态分布。
如何使用数据导入功能?
点击"选择文件"按钮或拖拽CSV/TXT文件到上传区域,工具会自动计算数据的均值和标准差并填充到输入框中。
支持哪些导出格式?
本工具支持导出结果为JSON、CSV格式,图表可导出为PNG、JPG和PDF格式。
如何解读计算结果?
概率密度(PDF)表示在特定X值处的概率密度;累积概率(CDF)表示X小于等于给定值的概率;分位数表示对应于给定概率的X值。
标准正态分布表怎么看?
标准正态分布表(Z表)用于查找标准正态分布的累积概率。使用时,先将原始分数转换为Z分数((X-μ)/σ),然后根据Z分数的整数部分和小数点后两位查找对应的累积概率。例如,Z=1.96对应的累积概率约为0.975,表示Z值小于等于1.96的概率为97.5%。
正态分布的期望和方差推导公式是什么?
对于正态分布N(μ, σ²),其概率密度函数为f(x) = (1/(σ√(2π)))e^(-(x-μ)²/(2σ²))。期望E[X] = ∫(-∞到∞) x*f(x)dx = μ,通过对称性可得。方差Var(X) = E[(X-μ)²] = ∫(-∞到∞) (x-μ)²*f(x)dx = σ²,通过变量替换和积分计算可得。
更新日期:
